Applied research on technical superconductors
Electromechanical properties
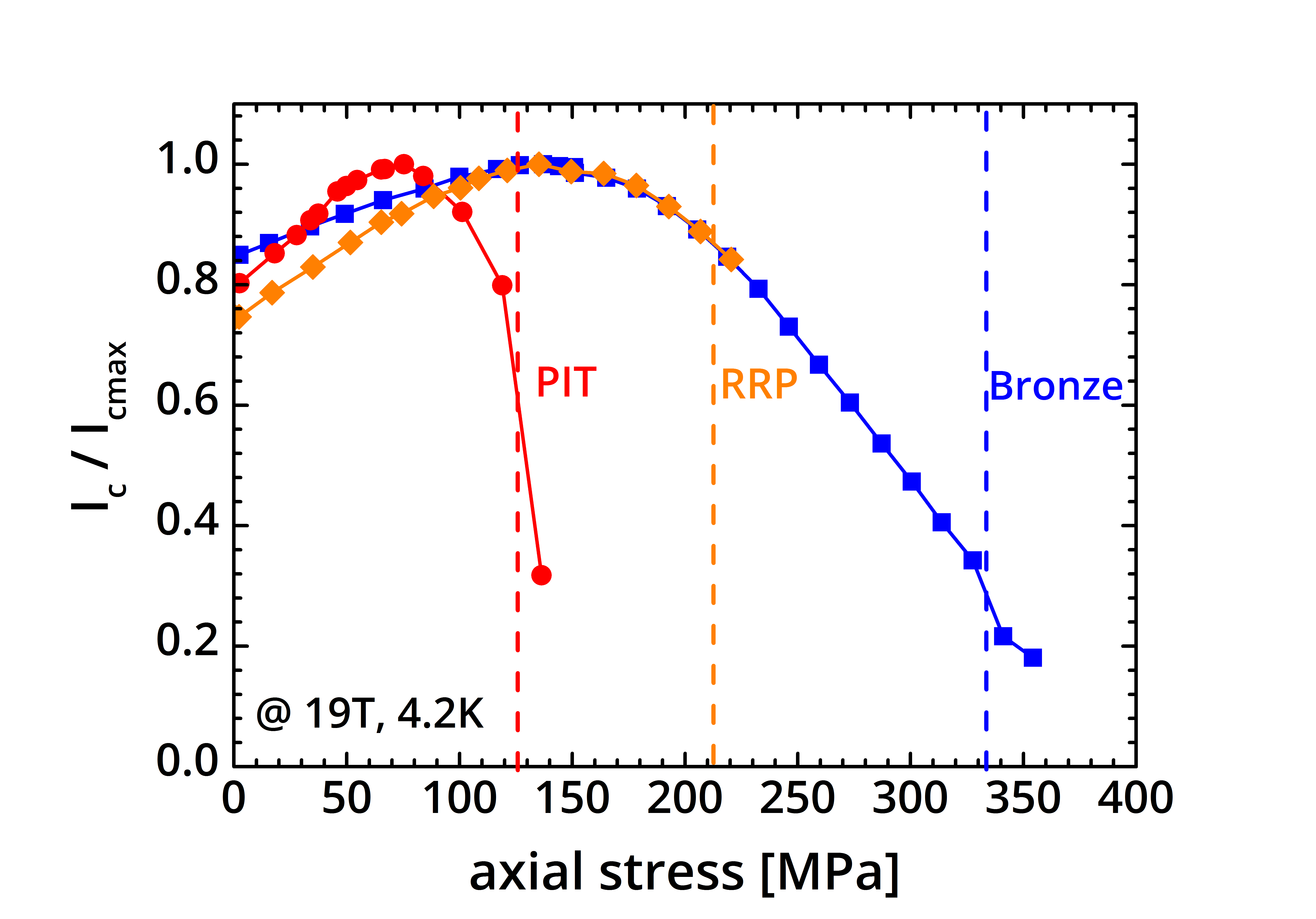
Stresses on superconductors arise mainly from two different sources: thermal contraction and magnetic forces. As the composite superconducting wire is cooled to the operating temperature, the mismatch in thermal contraction among the different components generates compressive strains on the superconductor, leading to large reduction of the critical current. On the other hand, when a superconducting magnet is energized, the magnetic Lorentz forces generate significant forces on the winding. The so-called magnetic hoop stress, acting along the axis of the conductor, increases in proportion to the intensity of the magnetic field and the radius of the winding. In large magnets, such as accelerator magnets and ITER coils, the conductors have to carry several kiloamps in high magnetic fields. In order to achieve the required current specifications, superconducting wires are arranged in cable configurations, Rutherford cables for the accelerator magnets, cable in conduit conductors (CICC) in the ITER coil design, respectively. In these arrangements, the superconductor experiences transverse stresses in addition to the hoop stress, as the Lorentz force determines wire-to-wire contacts and presses the wires against the containment structure.
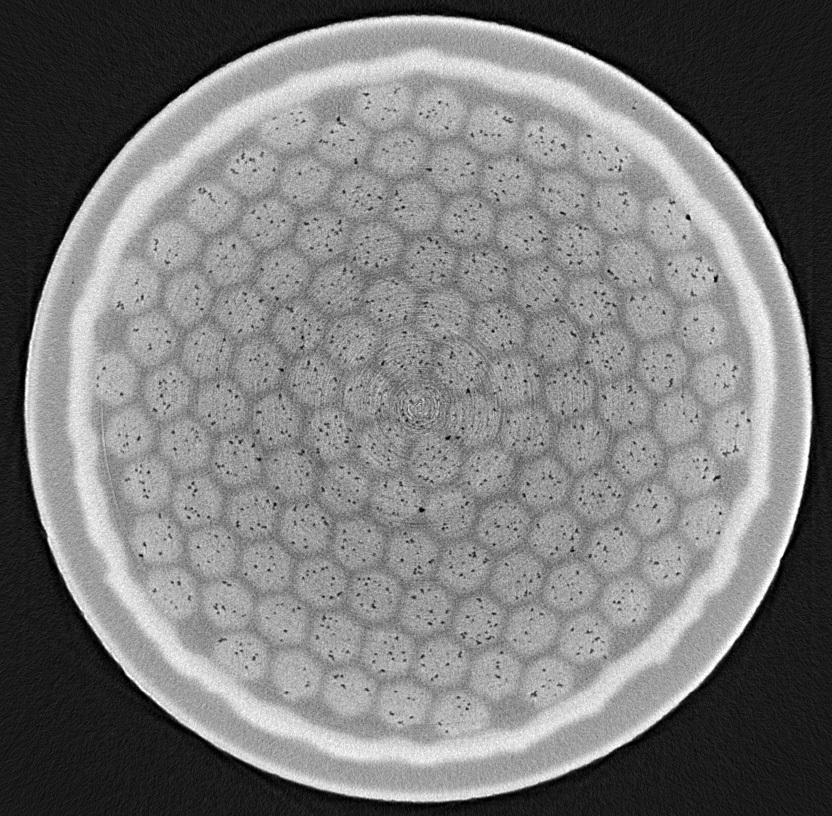
After applying a load, a reversible variation of the critical current of LTS and HTS wires occurs in a relatively wide range of applied strain, due to the strain dependence of the lattice elastic stiffness. Beyond a certain threshold, the critical current undergoes a permanent degradation because of cracks within the superconducting layer. A stochastic process is at the base of this phenomenon, related to the distribution of inhomogeneities in the microstructure of the superconductor. This is in turn determined by multiple parameters, as the wire fabrication technology and the reaction heat treatment conditions (temperature, duration, pressure). Our laboratory offers world-wide unique facilities to investigate the electromechanical properties of superconducting wires and tapes under different stress conditions. We implemented experiments to study the reversible and irreversible behaviour of the wires under axial and transverse stresses, using the concept of the Walters spring. As a complement to these studies, we perform synchrotron radiation X-ray microtomography experiments (link to a 3D reconstruction) for the three-dimensional visualization of voids and defects in the filament structure of multifilamentary superconducting wires. The goal is the improvement of the wire processing parameters, by establishing a quantitative correlation between the superconductor microstructure and the degree of irreversible wire degradation under mechanical loading.
Thermal stability and thermo-physical properties
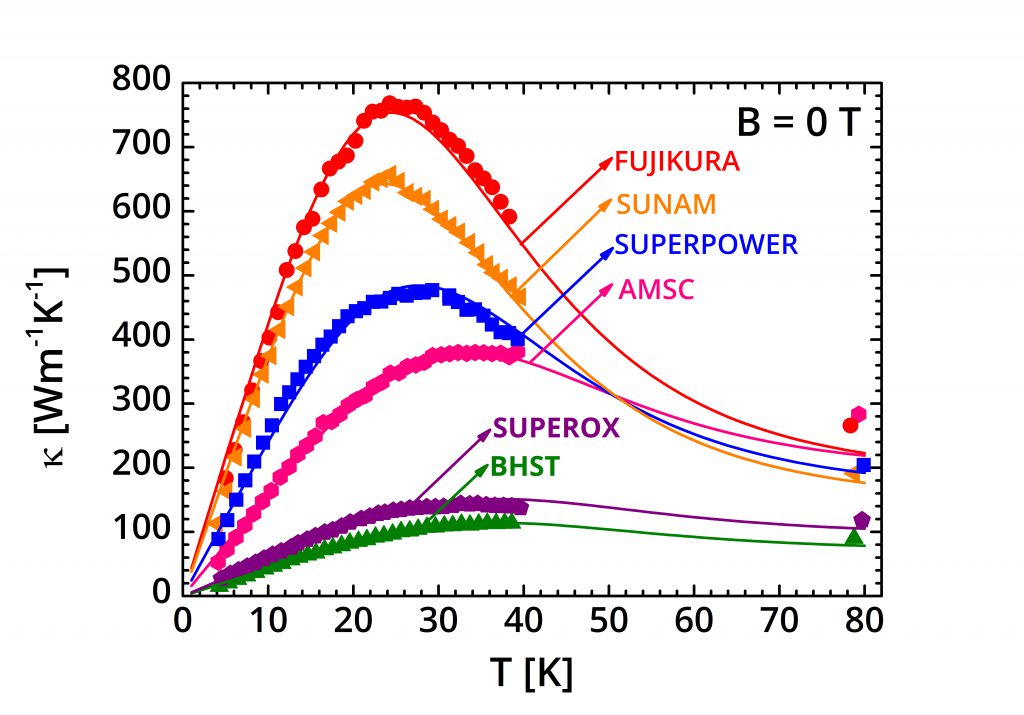
Thermal stability is one of the most important issues when designing a superconducting magnet. In order to increase the magnetic field intensity, B, as well as the bore diameter, higher operating currents are needed. The energy stored in a magnet scales with B2 and with the magnet volume. In case of thermal disturbance, this huge magnetic energy can be easily converted into heat. If the superconductor temperature rises locally above its critical value and the heat generation due to Joule effect overcomes the heat evacuated by the coolant, the normal zone will expand and eventually the whole magnet will revert to the normal state. This process is referred as a quench. A quench, in addition to damaging the winding thermally, may also do so mechanically by inducing localized strains. Being able to predict the response of the superconductor to a thermal disturbance is very important in order to protect the device from permanent damage.
Our focus is on the influence of the layout of technical superconductors, including the choice of the matrix materials, the type of stabilizer, the ratio between matrix and superconductor, etc., on the thermal transport properties. Heat capacity and thermal conductivity are measured at temperatures and magnetic fields reproducing the operating conditions of the real device and this provides us the primary ingredients for modelling – analytically and numerically – the quench behaviour.